摘要:针对OUR-2机械臂的构形特点,对其进行运动学及空间分析。采用D-H方法建立了OUR-2机械臂的连杆坐标系,得到了以6个关节角度为变量的正运动学方程,并用MATLAB robotics toolbox对机械臂的正运动学进行了仿真。基于蒙特卡洛法分析了机械臂的工作空间,并利用MATLAB编程得到机械臂末端的工作空间点云图。
关键词:OUR-2机械臂;D-H方法;正运动学;蒙特卡洛法
OUR机械臂有别于传统工业机械臂,其特点是体积小、重量轻、有很快的运动速度和较大的活动范围,机械臂的最大运动速度可以达到180°/s,能够处理更复杂、更危险的工作,具有极强的灵活度、精确度和安全性。
对于机械臂运动学而言,正运动学相对简单,机械臂的工作空间求解方法主要有图解法、解析法、数值法,以及由数值法衍生出来的蒙特卡洛法[1]。图解法和解析法受到关节数目的限制,对于有些机械臂并不通用;数值法计算量太大,有些边界曲面可靠性得不到保证[2]。蒙特卡洛法可以用数学图形的形式直观清晰地表示机械臂的工作空间。本文采用J.Craij改进的D-H方法建立机械臂的连杆坐标系,分析OUR-2机械臂的正运动学模型,得到机械臂正运动学的解析解,并利用MATLAB robotics toolbox进行正运动学仿真分析,运用蒙特卡洛法得到机械臂的工作空间。
1.1 机械臂模型
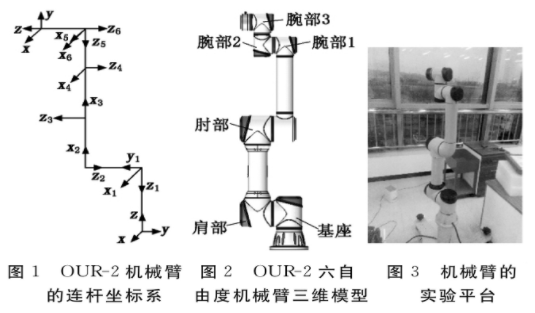
按照改进的D-H方法建立OUR-2六自由度机械臂的连杆坐标系。首先确定基坐标系的位置以及末端的初始位置和姿态,然后采用D-H法建立基坐标系和各关节处的坐标系,对于相同的基坐标系,不同的D-H矩阵的末端位姿相同。建立的OUR-2机械臂连杆坐标系如图1所示。
利用SolidWorks建立了OUR-2六自由度机械臂三维模型,如图2所示。机械臂共包括6个部分:基座、肩部、肘部、腕部1、腕部2以及腕部3。OUR-2有别于传统的六自由度机械臂,6个关节均为模块化旋转关节,每个模块均由高性能的伺服电机、谐波减速器、机械刹车、驱动器和通信总线组成,每个关节有一个自由度,机械臂的实验平台如图3所示。
1.2 机械臂正运动学分析
机械臂的工作空间是指机械臂末端所能到的范围,是机械臂灵活性的重要指标,理论上机械臂的工作空间是一个可以覆盖机械臂所在位置的球形区域[3],实际上由于奇点的存在,使得机械臂的灵活性和空间工作范围受到限制,如何扩大机械臂的工作空间以及增强它的灵活性是一个重要的研究方向。机械臂的运动学涉及末端位姿和关节变量,是空间分析的一个重要基础[4]。
根据OUR-2机械臂的连杆坐标系可以得到机械臂连杆参数,如表1所示。
表1 机械臂的连杆参数
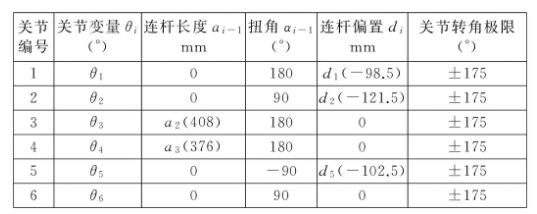
关节编号关节变量θi(°)连杆长度ai-1mm扭角αi-1(°)连杆偏置dimm关节转角极限(°)1θ10180d1(-98.5)±1752θ2090d2(-121.5)±1753θ3a2(408)1800±1754θ4a3(376)1800±1755θ50-90d5(-102.5)±1756θ60900±175
相邻连杆坐标系D-H变换矩阵为:
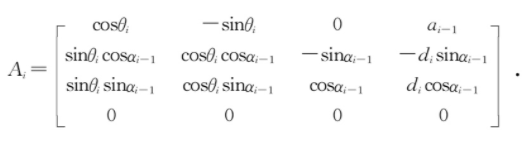
(1)
由表1以及D-H变换矩阵可以得到OUR-2机械臂的末端姿态:
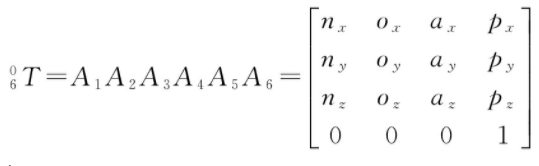
(2)
经过计算得到的基座和末端位姿的变换矩阵元素如下:
nx=-s6c1s432-c6(s1s5-c5c1c432),
ny=s6s1s432-c6(c1s5+c5s1s432),nz=-c5c6s432-s6c432,
ox=s6(s1s5-c5c1c432)-c6c1s432,
oy=s6(c1s5-c5s1c432)+c6s1s432,
oz=c5s6s432-c6c1c432,
ax=c5s1+s5c1c432,
ay=c5c1-s5c1c432,
az=-s5s432,
px=d2s1+a3c1c32-d5c1s432+a2c1c2,
py=d2c1-a3s1c32+d5s1s432-a2s1c2,
pz=a3s32-d5c432-a2s2-d1.
其中:sinθi=si;sin(θ3-θ2)=s32;cosθi=ci;cos(θ3-θ2)=c32;cos(θ4-θ3+θ2)=c432;sin(θ4-θ3+θ2)=s432。
1.3 OUR-2机械臂正运动学仿真
MATLAB robotics toolbox是一个功能强大的工具箱,可以对机械臂进行运动学、轨迹规划、动力学等方面的仿真[5]。
MATLAB robotics toolbox的drivebot(r)命令可以生成OUR-2机械臂的三维模型,同时生成机械臂控制面板,控制面板可以调节机械臂的角度,从而使关节产生转动。
设置仿真的初始关节变量和终止关节变量以及仿真时间,此时可以得到机械臂的末端位姿以及末端姿态矩阵。当初始角度θ初=(0,-π/3,π/6,π/2,0,0),终止角度θ终=(π/6,-π/6,π/3,-π/3,0,0)时,可以得到机械臂的初始和终止三维模型,如图4所示。
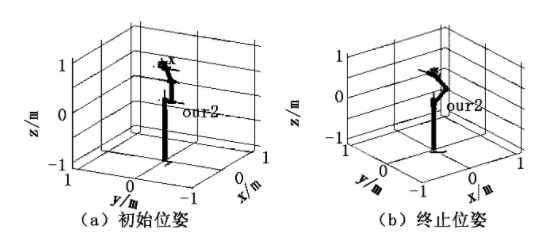
图4 机械臂的初始和终止三维模型
由于5、6关节角位移并没有变化,这里不再列出其角位移曲线,利用MATLAB编程可以得到前4个关节的角位移曲线,如图5所示,末端执行器的运动轨迹如图6所示。
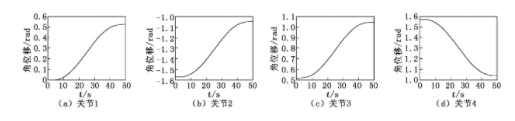
图5 前4个关节的角位移曲线
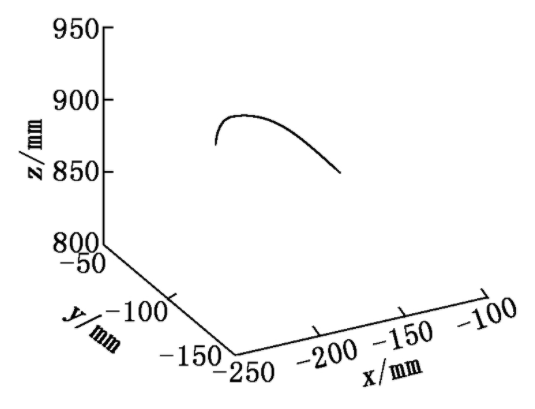
图6 末端执行器的运动轨迹
图5表明了机械臂各关节运行正常,可以平稳地从初始位置到达终止位置。图6表明了OUR-2机械臂的参数设置合理,可以达到预期的目标。
机械臂的工作空间是指机械臂正常运行时,末端执行器坐标系的原点能在空间活动的最大范围,或者说该原点可达点占有的体积空间,这一空间又称可达空间或总工作空间[6],记作W(p)。关节变量和工作空间的关系可表示为:
W(p)={P(θi,θi∈Q)}.
其中:θi为关节变量,θi=[θ1,θ2,θ3,θ4,θ5,θ6];Q为空间约束,Q={θ‖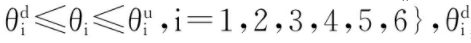 和
和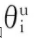 分别为关节运动的下限和上限。因此,机械臂的工作区域可以表示为:
分别为关节运动的下限和上限。因此,机械臂的工作区域可以表示为:
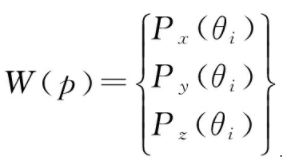
(3)
蒙特卡洛法是一种利用随机抽样解决数学问题的方法,其计算速度快,工作量小,能够精确地绘制出计算机图形,利用蒙特卡洛法求取工作空间的具体步骤如下[7]:
(1) 对OUR-2机械臂进行正向运动学分析,得到机械臂的末端姿态向量。
(2) 利用随机函数Rand(j)产生N个随机值(0~1之间),由此产生的随机步长为(θimax-θimin)·Rand(j)(θimax和θimin为关节变量的上限和下限),可以得到机械臂各个关节转角的伪随机值为θi=θimin+(θimax-θimin)Rand(j)。
(3) 将 6个关节转角代入正运动学方程,得到机械臂末端的坐标值,所求末端位置点数目越多,机器人的实际工作空间反映得越精确。
(4) 利用MATLAB强大的画图功能,将所得位置用点的形式表现出来,便可得到工作空间的“云图”。三维云图代码如下:
xx = ;
yy = ;
zz = ;
for N = 1:10000
N
a1=(175*(2*rand(1)-1))*pi/180;
a2=(175*(2*rand(1)-1))*pi/180;
a3=(175*(2*rand(1)-1))*pi/180;
a4=(175*(2*rand(1)-1))*pi/180;
xx=[xx,-121.5*sin(a1)+376*cos(a1)*cos(a3- a2)+102.5*cos(a1)*sin(a4-a3+a2)+408*cos(a1)*cos(a2)];
yy=[yy,-121.5*cos(a1)-376*sin(a1)*cos(a3-a2)-102.5*cos(a1)*sin(a4-a3+a2)-408*sin(a1)*cos(a2)];
zz=[zz,376*sin(a3-a2)+102.5*cos(a4-a3+a2)-408*sin(a2)+98.5];
end
figure(1);
plot3(xx,yy,zz,'g.');
其中:a1=θ1;a2=θ2;a3=θ3;a4=θ4;xx、yy、zz为机械臂的空间位置向量。
本文取N=100 000,即随机坐标数目为100 000个,应用蒙特卡洛法可得机械臂的工作空间云图,如图7所示。
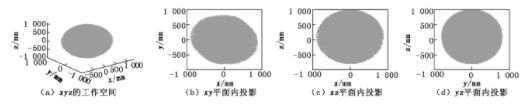
图7 机械臂的工作空间云图
由图7可以看出,OUR-2机械臂几乎可以达到最大区域的所有空间,利用蒙特卡洛法仿真模拟可以得到一系列的随机点,但与真实的工作区域还有一定差距,这是由于该方法本身的限制,利用蒙特卡洛法只能不断地逼近真实工作区域,并且这种逼近程度随着关节组合数量越多越接近真实工作区域[8]。
本文首先分析了OUR-2机械臂的正运动学方程,利用MATLAB robotics toolbox进行了运动学仿真,验证了结构的合理性。然后基于蒙特卡洛法进行了空间分析,可以看到空间内部点分布均匀,满足机械臂的使用要求。蒙特卡洛法克服了几何法受到自由度限制的缺陷,并且能够精确反映机械臂的工作空间。